

PERSAMAAN DIFFERENSIAL BIASA DENGAN METODE EULER

Persamaan differensial adalah pesamaan yang memuat turunan satu (atau beberapa ) fungsi yang tidak diketahui.

Suatu persamaan diferensial yang terdiri dari satu variabel bebas saja dinamakan perasamaan diferensial biasa (Ordinary Differential Equation-ODE). Penyelesaian persamaan deferensial biasa dengan metode Euler adalah proses mencari nilai fungsi y(x) pada titik x tertentu dari persamaan deferensial f(x,y) yang di ketahui dengan menggunakan persamaan umum persamaan 2. Penyelesaian persamaan diferensial biasa (ODE) mempunyai bentuk umum yaitu :

Metode euler atau disebut juga metode orde pertama karena persamaannya kita hanya dapat mengambil sampai suku orde pertama saja.

CONTOH

Membuat program untuk menyelesaikan persamaan differensial biasa berikut dengan menggunakan metode Euler

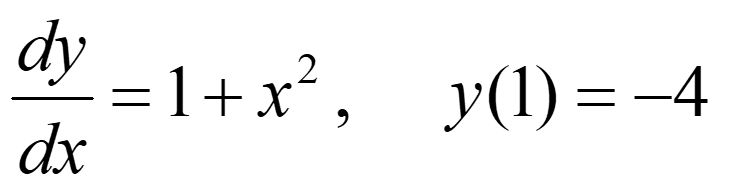
untuk menentukan y(1.01), y(1.02) dan y(1.03).

PROGRAM PYTHON

print("f(x,y)=1+x^2")
print("yi+1 = y1 + hf(xi+yi)")
x1 = float(input("Masukkan x1= "))
x2 = float(input("Masukkan x2= "))

h = 1.01-x1 #Langsung saya atur sendiri karena yang dicari f(x,y) nilai x-nya=1.01
n=4 #jumlah x ada 4 yaitu 1, 1.01, 1.02, 1.03
xi = -4
hasil = xi
y=0
for i in range(n):
    print("hasil dari y"+str(i)+"= "+ str(hasil))
    hasil = xi + h*(1+(x1+y)**2)
    y+=h
    xi=hasil

Pada bagian pertama terdapat variable x1 adalah x awal dan x2 merupakan x akhir. karena di soal terdapat nx=3 yaitu x0=1, x1=1,01, x3=1,02 x2=1,03 maka h= xn-x0/n, hasilnya h = 0.01.

xi adalah hasil awal yang kemudian akan dimasukkan pada prosess iterasi. Karena rumus eurel adalah y1 = y0 +h(f(x,y)) maka rumus barunya adalah y1=y0+h(1+x^2). variable y digunakan untuk penambahan nilai x agar selalu bertambah 0.01.